PCA Explained Simply
Hi! If you are reading this, you are either:
- not a data scientist but want to understand why PCA should be used
- a data scientist but want to explain to a colleague why PCA should be used
I recently realised that explaining Principal Component Analysis (PCA) to non-scientists is a universally common experience that all data scientists eventually do.
I will explain when PCA is needed, what PCA does, an example with PCA, what benefits PCA brings, and how to interpret the results of PCA.
I will not detail how PCA works, how to use PCA, or whether to use PCA or other methods, but I link nice resources in the FAQ.
If you have questions not addressed in the FAQ, please leave a comment and I will answer you.
Why is PCA needed?
PCA reduces the number of dimensions of the dataset.

Thus, PCA is needed if you:
- have a very high-dimensional dataset (e.g. ≥100 features)
- cannot afford a large amount of compute (minutes vs hours vs days)
- want to make sense of many features (e.g. to select important features)
By applying PCA, you:
- save time (during model training and model iteration)
- save space (in memory and model parameters)
- trade-off a little bit of performance
What does PCA do?
In a sentence:
PCA produces new features as a weighted sum of the original features in the dataset, by preserving variance in the original features.
What is a weighted sum?
\[X = w_1\cdot x_1 + \dotsb + w_n\cdot x_n\]\(X\) is a sum of values \(x_1,\dotsc, x_n\), each weighted by \(w_1,\dotsc, w_n\) respectively. Likewise, PCA produces new features, e.g. \(X_1, X_2,\dotsc\), as weighted sums of original features \(x_1,\dotsc, x_n\).
Why preserve variance?
Preserving variance in the original features retains information about the spread of features in the data, usually resulting in good representations of original features for machine learning.
Show me an example!
Let’s walk through PCA with the Boston Housing dataset:
Given a dataset of 37 numerical features of houses, you want to predict its sale price. However, dealing with so many features can be (imagine) expensive in compute and difficult to interpret.
Code
import pandas as pd
!kaggle competitions download -c house-prices-advanced-regression-techniques
!unzip house-prices-advanced-regression-techniques.zip
train = pd.read_csv('train.csv')
df = train._get_numeric_data().dropna()
df.head()| Id | MSSubClass | LotFrontage | LotArea | OverallQual | OverallCond | YearBuilt | YearRemodAdd | MasVnrArea | ... | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 60 | 65.0 | 8450 | 7 | 5 | 2003 | 2003 | 196.0 | ... | 208500 |
| 1 | 2 | 20 | 80.0 | 9600 | 6 | 8 | 1976 | 1976 | 0.0 | ... | 181500 |
| 2 | 3 | 60 | 68.0 | 11250 | 7 | 5 | 2001 | 2002 | 162.0 | ... | 223500 |
| 3 | 4 | 70 | 60.0 | 9550 | 7 | 5 | 1915 | 1970 | 0.0 | ... | 140000 |
| 4 | 5 | 60 | 84.0 | 14260 | 8 | 5 | 2000 | 2000 | 350.0 | ... | 250000 |
5 rows x 38 columns
Because PCA reduces the number of dimensions of the dataset, model training can take a shorter time without sacrificing too much performance.
Let’s run PCA on the 37 features:
Code
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
X = df.drop(columns='SalePrice').values
y = np.log(df['SalePrice'])
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
pca = PCA(n_components=2)
pca.fit(X_train)
X_features = pca.transform(X_train)
X_features_test = pca.transform(X_test)
print("Original features (normalized):\n", X_train[0].round(3))
print("\nPCA features:\n", X_features[0].round(3))Original features (normalized):
[-0.646 0.136 0.171 -0.252 1.297 -0.523 1.221 1.129 0.026 0.221
-0.283 -0.675 -0.531 -0.856 1.734 -0.106 0.784 1.175 -0.233 0.79
1.238 0.175 -0.202 0.9 -0.943 1.214 0.211 0.271 -0.746 1.613
-0.363 -0.114 -0.285 -0.074 -0.146 2.113 0.879]
PCA features:
[ 2.141 -1.273]
What benefits does PCA bring? At what trade-off?
Let’s train 2 linear regression models:
- Trained on the original 37-dimensional features
- Trained on the 2-dimensional features produced by PCA
Performance: A Tiny Trade-off
Even though PCA reduces the number of dimensions from 37 to merely 2, there is a small decrease in test error of only -0.02 (RMSE of log of sale price as evaluated on Kaggle).
Code
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lr = LinearRegression()
lr.fit(X_train, y_train)
y_train_hat = lr.predict(X_train)
y_hat = lr.predict(X_test)
print("Original Features (37 dimensions)")
print("Train error:", np.sqrt(mean_squared_error(y_train, y_train_hat)).round(4))
print("Test error:", np.sqrt(mean_squared_error(y_test, y_hat)).round(4))
lr_pca = LinearRegression()
lr_pca.fit(X_features, y_train)
y_train_hat = lr_pca.predict(X_features)
y_hat = lr_pca.predict(X_features_test)
print("\nPCA features (2 dimensions)")
print("Train error:", np.sqrt(mean_squared_error(y_train, y_train_hat)).round(4))
print("Test error:", np.sqrt(mean_squared_error(y_test, y_hat)).round(4))Original Features (37 dimensions)
Train error: 0.15
Test error: 0.1348
PCA features (2 dimensions)
Train error: 0.1935
Test error: 0.1562
Training Time: A Major Speed-up
With PCA, because number of features is drastically reduced (from 37 to 2), training time taken is also reduced from 4.85ms to 584µs, a 8300X speedup!
Code (Linear regression with original features)
%%timeit
lr = LinearRegression()
lr.fit(X_train, y_train)
y_train_hat = lr.predict(X_train)
y_hat = lr.predict(X_test)4.85 ms ± 276 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Code (Linear regression with PCA features)
%%timeit
lr_pca = LinearRegression()
lr_pca.fit(X_features, y_train)
y_train_hat = lr_pca.predict(X_features)
y_hat = lr_pca.predict(X_features_test)584 µs ± 19 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
Memory Space: A Significant Reduction
Because the no. of dimensions decreased by 18.5X, so did memory space used, from 265Kb to 14Kb.
Code
print(f"Memory size of data w/o PCA: {X_train.size * X_train.itemsize} bytes")
print(f"Memory size of data w/ PCA: {X_features.size * X_features.itemsize} bytes")Memory size of data w/o PCA: 265216 bytes
Memory size of data w/ PCA: 14336 bytes
How to interpret PCA results
Recall what PCA does:
PCA produces new features as a weighted sum of original features, by preserving variance in the original features.
PCA produces new features, \(X_1, X_2\) as a weighted sum of the original features, \(x_1, x_2, x_3\).
In other words, we can get \(X_1\) and \(X_2\) using \(PC_1\) and \(PC_2\), by computing a weighted sum of \([x_1, x_2, x_3]\).
\[X_1 = w_{11}x_1 + w_{12}x_2 + w_{13}x_3\] \[X_2 = w_{21}x_1 + w_{22}x_2 + w_{23}x_3\]Compare weighted sums with PCA features:
Code
print("PC1 weighted sum:", sum(pca.components_[0] * X_train[0]).round(3))
print("PC2 weighted sum:", sum(pca.components_[1] * X_train[0]).round(3))
print("PCA features:", X_features[0].round(3))PC1 weighted sum: 1.515
PC2 weighted sum: 0.968
PCA features: [1.515 0.968]
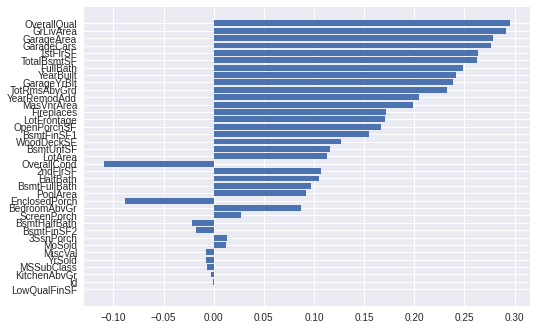
Inspecting principal component 1, the highest weighted feature is OverallQual. This means that OverallQual has the highest variance of all features in the dataset, and is likely a useful feature for sale price prediction.
Sort features by the 1st principal component’s weights:
Code
import matplotlib.pyplot as plt
plt.style.use('seaborn')
i = np.abs(pca.components_[0]).argsort()
pca_component_1 = pca.components_[0][i]
columns = df.drop(columns='SalePrice').columns[i]
plt.barh(columns, pca_component_1)
plt.show()